Why rebalance? A simple statistical story (part I)

Once we have picked an asset allocation model, how often, or why should we rebalance? I’ve seen multiple conflicting findings about the usefulness of rebalancing. Many such conflicts happen in time-series data because the sample you use can influence things quite strongly. I therefore wanted to see if there was a simple, purely statistical basis for rebalancing.

To do this, I simulated some pretty vanilla portfolios with the desired characteristics. Note that as this isn’t real data, it doesn’t have some of the finer characteristics of true returns data such as auto-correlation of volatility.

Method

1. Create a portfolio of three assets:

1
2
3
4

  expected_returns <- c(0.01, 0.03, 0.06)
  vol <- expected_returns * 2
  corrs <- matrix(0.3) # Correlation matrix
  weights <- (0.4, 0.3, 0.3) 

2. Simulate 300 such portfolios over 5 years, monthly periods.
3. Take the mean and volatility of the portfolios.
4. Vary frequency of rebalancing to the correct weights.

Results:

1. The expected return goes up by not rebalancing. This is likely because without rebalancing, over time the higher expected return assets make up a larger proportion of the portfolio, which increases the expected returns overall.

2. However, the volatility of the portfolio goes up as you rebalance less frequently as well. In fact, it goes up faster, so that the return per volatility decreases.

3. The return/volatility decreases by about 0.3 per year you wait to rebalance. Nothing huge, but nothing to ignore either.

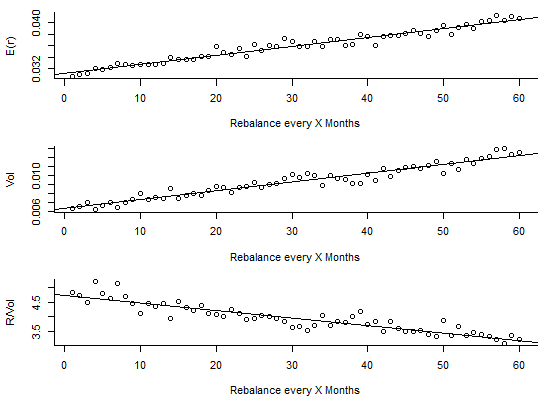
So on purely statistical grounds, rebalancing appears to be helpful. But can we improve upon this?

1. We can specify thresholds which the individual asset classes shouldn’t breach, or when they do, we rebalance back at that point.

2. We can use recent market movements to indicate things which are expensive vs cheap, and purchase accordingly.

Next time!

R Code here